Introduction
Most animals exhibit an escape behavior that accelerates rapidly when exposed to sudden predation threats (Bisazza et al., 1997; Tay et al., 2021; Webb, 1986). It is important to understand the kinematic characteristics (e.g., flight initiation distance, escape trajectory, turning speed, and acceleration) of the escape behavior, as this is crucial to the survival of the individual and the suitability of the species as well as to understand stability parameters of the predator-prey system. The kinematic characteristics are strongly influenced by the physiological state of the individual but are also governed by external environmental factors. Thus, the characteristics have been explored in relation to physiological and environmental factors (Bateman & Fleming, 2014; Colwill & Creton, 2011; Domenici, 2002; 2010; Ozel & Stynoski, 2011; Paul et al., 2021). Most of these studies have been conducted on vertebrate animals and have provided an understanding of animal escape behavior. However, in recent years, ethical restrictions related to animal experiments have been strengthened, resulting in limited research.
Research using fish is relatively free from ethical issues, and easy to observe and analyze the behavior. For this reason, research on escape behavior in fish has attracted much attention from diverse academic perspectives such as neurophysiology (Eaton et al., 2001), biomechanics (Wakeling, 2006), kinematics (Domenici & Hale, 2019), and behavioral ecology (Binning et al., 2014; Godin, 1997). In particular, from a behavioral ecology point of view, Domenici (2010) suggested that when prey escape, they behave in the direction of minimizing the cost function defined by an economic theory developed by Ydenberg and Dill (1986) and Lima and Dill (1990). The cost function includes various physical quantities and the response distance at which the prey begins to escape the predator (Domenici et al., 2007): predator approach speed (Cooper, 2003; Cooper et al., 2003), directness of approach (Burger & Gochfeld, 1990; Cooper, 1997; 2010), persistence in attacking (Cooper & Avalos, 2010), direction of refuge relative to the predator (Cooper & Wilson, 2007). In addition, studies on the escape behavior of fish are directly related to the conservation of fishery resources for environmental pollution and environmental protection (Brodin et al., 2014; Jacquin et al., 2020). Thus, we have come to understand the various kinematic characteristics of the escape behavior of fish. However, there is still a lack of research which quantitatively characterizes the escape behavior of fish in relation to the attack patterns of aerial predators (birds). This is because it is not easy to define a statistical quantity that can characterize the attack patterns, and it is technically difficult to measure changes in fish behavior that occur in a short period of time.
In this study, I explored the escape behavior of the medaka fish, Oryzias latipes, in response to the attack of a model bird of three different sizes and attack speeds. Species that actually feed on medaka fish include herons and kingfishers (Naher, 2015). In other words, this study is an analysis of the response behavior of medaka fish to the predator species. To characterize this escape behavior, I used five physical variables: escape speed, escape acceleration, responsiveness, branch length similarity (BLS) entropy, and degree of alignment of fish groups. The escape speed, acceleration, and responsiveness are physical variables reflecting the kinematic characteristics of the fish, and the BLS entropy and alignment are variables that reflect the static characteristics of the fish. These variables not only help quantify escape behavior but also to develop mathematical models that can simulate the escape behavior.
In particular, it will be useful to determine the variables that should be applied in a model and to estimate the values of those variables. I constructed vectors comprising these five variables and classified them into two groups with similar characteristics. Using this classification, I briefly discussed the idea for characterizing the threat to the fish generated from the approach of predators.
Materials|Methods
Test species and the observation system
Two hundred and fifty Medaka fish (Oryzias latipes) were housed in a circular water tank 100 cm in diameter and 30 cm in height. Prior to the experiment, the fish were acclimated to the experimental conditions (12 h light:12 h dark photoperiod at 20°C water temperature) for 4 weeks. Fish were provided TetraMin (Tetra Werke, Melle, Germany) flake food (1 g/day) daily. The average length of the fish was 20.74±2.19 mm.
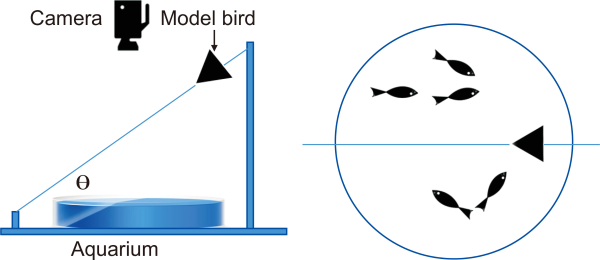
I placed 20 fish in a tank filled with water (water depth of 5 cm) and investigated how the fish escape when model birds of different sizes and speeds approach them. To simulate the approach, the model bird, made of a triangular-shaped acrylic plate, was attached to a fishing line connected between two rods at either end of the water tank. The triangular shape was set to 10×15 (S=1), 15×20 (S=2), and 20×25 cm (S=3) with base×height. The slope (θ) of the fishing line was set to values of 15° (θ=1), 30° (θ=2), and 45° (θ=3) (Fig. 1).
During the experiment, I protected the laboratory from external stimuli such as sound and light. A digital camcorder (SONY CX-550; SONY, Tokyo, Japan) equipped with a wide-angle lens (Raynox QC-505; Raynox, Tokyo, Japan) to obtain a clear image was fixed at a height of 120 cm from the bottom of the tank to observe fish escape behavior. For the acclimatization of the fish to the environment before performing the experiment, I left the fish for 2 hours without external stimulation. After the acclimatization time, the fish’s movements became stable without sudden rapid movements. I recorded a set of 10 replicates for a combination of size and angle of a model bird to obtain statistical results on fish escape behavior. I extracted 4-sec video clips of the escape behavior from the recordings. The video resolution was 1/10 seconds (Fig. 2).
Analysis
The escape behavior was characterized using five variables: escape speed (v), escape acceleration (α), responsiveness (γ), BLS entropy (ε), and alignment (φ). I defined the escape time as the time taken for the model bird to pass over the water tank in which the fish were placed. The time varied slightly depending on the slope of the model bird, but it was approximately 0.4 seconds. The escape behavior of fish is performed either through direct sensing of the presence of a predator or through information transmitted in the form of rapid behavioral changes (e.g., speed and direction) of neighboring mates (Eaton et al., 1981; Gerlotto et al., 2006). During the performance period, the fish’s behavior (fast-start response) is triggered by a pair of higher-order neurons, commonly called Mauthner cells. The fast-start response is one of the main behavior that increase the chances of survival from predators. For this reason, the escape response time was set to 0.4 seconds and the analysis of fish behavior after the escape period was excluded. The v (α) was defined as the average value of the v (α) during the escape period. These variables reflect the degree to which fish recognize a model bird as a threat (Bulova, 1994; Cooper, 1997; 2003). The γ represents the ratio of the number of individuals responding to the model bird to the total number of individuals (=20) during the escape period (Fuiman et al., 2006). If γ has a value of 1, it indicates that all individuals escaped from the model bird, whereas if γ has a value of 0, it represents that no individuals responded to the attack of the model bird.
The ε shows how fish are distributed when viewed from the center of the water tank (Lee, 2010). The ε was defined in a simple network comprising a single node and its branches as below (see Fig. 3),
Here, the probability of the i-th branch of the simple network is defined as
where n is the number of branches in the simple network and Lk is the length of the k-th branch (k=1, 2, 3, …, n). The denominator log(n) is introduced to normalize the entropy. In this study, I used the distance from the center of water tank to each fish individual as the branch length. When the value of ε is approaching 1.0, it means that all the branch lengths are the same, and smaller the entropy value, the more heterogeneous is the length distribution. This variable measures the degree to which fish disperse when escaping.
The variable for the alignment of the fish group (φ), indicates how all individuals are aligned in one direction. This variable was mathematically defined by the absolute value of the average unit velocity of fish (Lee, 2006);
where Ntot (=20) was the total number of fish individuals and vj was the unit velocity vector of the j-th individual (j=1, 2, 3,…, 20). If φ=1, then all fish individuals are headed in one direction, and if φ=0, all individuals have random orientation.
Results
The speed at which the model bird moved along the line was 1.48±0.13 m/s, 3.10±0.18 m/s, and 4.49±0.34 m/s for θ=15°, 30°, and 40°, respectively. Table 1 shows the characterization values of the fish escape behavior. The values were obtained under the condition of (S, θ)=(fixed, 1:3). The results showed there was no statistical change in the escape behavior with the change in falling slope within each size category of model birds. This means that the fish are not sensitive to the approach speed of the model bird, at least in the range of 15-45°.
Table 2 shows how the fish responded to the size of the model bird (S) when the θ was fixed. In the case of θ=1, the v, α, and γ increased as S increased. This can be interpreted as the fish responded more sensitively to the size of the model bird. That is, as the size of the model bird increased, the degree of the threat increased. The increase in γ can be easily understood from the fact that the larger the size of the model bird, the easier it is for more individuals to recognize the bird. When S increased, the fact that ε decreased and φ increased showed a tendency that the distance between individuals was not maintained with the increased sense of threat, but the degree of alignment with direction tended to be stronger.
For θ=2, all variables for S=1 and 2 were statistically identical. Thus, fish did not distinguish between model birds with S=1 and S=2. At S=3, all variables except ε were increased. Thus, the fish responded strongly to the approach of the model bird and showed a tendency to keep the interval between the individuals constant during the escape. In other words, it indirectly showed that unchanged ε values are one of the intrinsic characteristics that appear irrespective of the degree of threat to the fish.
In the case of θ=3, the values of φ and ε did not change with respect to the increase of S, whereas the increase of v, α, and γ was observed. Thus, as the model bird approached quickly, fish individuals strengthened their tendency to align and the tendency to maintain a constant spacing among individuals.
Based on the data shown in Tables 1 and 2, the change in values of the five variables indicated that fish became more threatened when the size of the model bird became larger. To clarify this, I performed the k-means clustering algorithm (Oyelade et al., 2010). A vector defined by the five variables for each case of (S, θ) was constructed. I calculated the silhouette scores for the number of groups from 2 to 10 and examined how many of these total vectors would be best grouped (Table 3). The silhouette score is an indicator of how well the grouping has performed. The higher the score, the better is the grouping. The results showed that the best grouping was performed when the number of groups was 2. Table 4 shows the percentage of vectors belonging to group 1 or 2. The vectors for S=3 were included in group 1, while the vectors for S=1 were included in group 2. The vectors for S=2 belonged to both groups 1 and 2. The grouping results showed the escape behavior can be divided into two groups; one being highly threatened with predators and the other being less threatened. In other words, the vectors belonging to group 1 represent escape behavior associated with less threat and the vectors belonging to group 2 represent escape behavior associated with greater threat.
Discussion
In the field, the attack speed of the predator towards the prey varies greatly depending on the species and the degree of hunger of the predator (Domenici, 2002). In the preliminary investigations, when the falling slope was made smaller than 15°, only 2-3 fish responded to the model bird and when the slope was larger than 45°, the escape behavior appeared after the model bird passed. Thus, I selected three angles, 15°, 30°, and 45°, in the range within which more than 10 fish responded.
In this study, I dropped the model birds when all the fish were at rest and most of the fish individuals were located beneath the drop of the model bird. The reason for this is that individuals scattered throughout the water tank are likely to notice different sizes of model birds owing to different angles with the model birds. Moreover, in many cases, the bird attack does not follow a straight line at a constant speed. This is because the bird attempts to minimize air resistance by wind or to obtain strategic advantages for moving prey (Tucker et al., 2000). Therefore, the escape behavior of fish in the field is likely to be different from the experimental results of this study. It would be interesting to explore the escape behavior of fish by allowing model birds to fall along a curved, rather than straight, path.
The statistical values of v, α, γ, ε, and φ can be useful information in constructing machine learning-based models, such as hidden Markov models (HMM). This is because the variables contain information on both the dynamic and static characteristics of the escape behavior. An HMM is characterized by two stochastic processes: processes in the invisible hidden state and processes seen as time series of observable events. The invisible state is defined by a finite number of states, an initial state probability distribution, and a state transition probability matrix (TPM). On the other hand, the observable state is defined as a set of probability density functions related to the probability of occurrence (emission probability matrix, EPM). The former process is to optimize the structure of the model to efficiently learn the observation data obtained from the experiment. Therefore, this process can be algorithmically optimized. The latter process, however, should define variables characterizing the time-dependent phenomena. The performance of the HMM depends considerably on variables defining the behavioral state. Therefore, setting the variable plays a very important role in the ability of HMM to learn the sequence of states comprising the variables. The HMM (composed of TPM and EPM) for fish escape behavior allows us to numerically quantify changes in the behavioral characteristics of fish. In other words, since the structures of the two matrices can vary sensitively with different types and ages of fish, we can characterize behavioral changes for different species and ages through the structural analysis.
In this study, I classified fish escape behavior into two types using k-means clustering algorithm: one is that the fish feel strongly threatened and the other is that the fish feel relatively weakly threatened. If we have the information of v, α, γ, ε, and φ for a new fish’s escape behavior, we can statistically determine whether this fish feels a great threat from the predator or a minor threat. An easy way to make this determination is to use the k-nearest neighbor algorithm (Bailey & Jain, 1978). This algorithm tells you which vectors are located around any one vector within a given set of vectors. Thus, we can know how many vectors, belonging to group 1 or group 2, exist around the vectors generated by the five variables of the new fish. If there are more vectors belonging to group 1 (or 2) then the new vector can be determined to belong to group 1 (or 2).
In this study, the escape behavior was divided into only two groups because the number of repetitions of experiments was small. The results imply that the type of escape behavior is mainly determined by the size of the model bird. In this respect, when the prey fish schooling size is large, it can be understood to some extent that their predators avoid aggressive attacks. However, if more experiments could be added, the escape behavior would be divided into several groups and the escape behavior characterized more specifically.
I believe that this study is meaningful not only in that it provides essential data for the development of a fish schooling simulation model, but also in that it provides an approach that can be used to quantitatively analyze the escape behavior of various fish species.
Figures and Tables
Fig. 2
Model bird passing over a water tank and an escaping fish. The blue circle at t=0 (s) represents the position of fish before the model bird passes, the white circle at t>0 (s) represents the initial position of the fish, and the blue circle represents the later position after the escape behavior. The arrows represent the vector from the initial position to the later position.
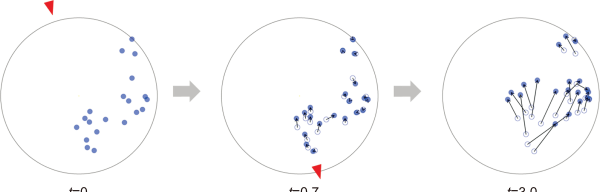
Fig. 3
Branch length similarity entropy definition on a network comprising one node and several edges.
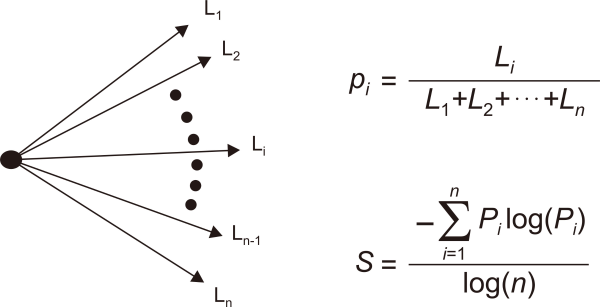
Table 1
Statistical values of the five physical variables for fish escape behavior for model birds with size S and falling angle θ under the condition that S is fixed and θ changes
| S | θ | v (speed) | α (acceleration) | γ (responsiveness) | ε (BLS entropy gradient) | φ (alignment) |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.104±0.047a | 0.033±0.028a | 0.221±0.037a | 1.000±0.000a | 0.393±0.066a |
| 2 | 0.111±0.033a | 0.038±0.011a | 0.251±0.053a | 0.954±0.095a | 0.470±0.094a | |
| 3 | 0.103±0.039a | 0.031±0.010a | 0.243±0.093a | 0.933±0.190a | 0.434±0.063a | |
| 2 | 1 | 0.225±0.058a | 0.047±0.022a | 0.363±0.073a | 0.797±0.220a | 0.512±0.119a |
| 2 | 0.152±0.025a | 0.040±0.007a | 0.304±0.037a | 0.930±0.088a | 0.490±0.078a | |
| 3 | 0.156±0.074a | 0.039±0.010a | 0.315±0.127a | 0.939±0.072a | 0.466±0.166a | |
| 3 | 1 | 0.317±0.077a | 0.071±0.019a | 0.473±0.066a | 0.719±0.194a | 0.655±0.088a |
| 2 | 0.223±0.046b | 0.058±0.012a | 0.389±0.054a | 0.892±0.190a | 0.609±0.070a | |
| 3 | 0.199±0.044b | 0.062±0.016a | 0.431±0.071a | 0.875±0.231a | 0.562±0.109a |
Table 2
Statistical values of the five physical variables for fish escape behavior for model birds with size S and falling angleθ under the condition that θ is fixed and S changes
| θ | S | v (speed) | α (acceleration) | γ (responsiveness) | ε (BLS entropy gradient) | φ (alignment) |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.104±0.047a | 0.033±0.028a | 0.221±0.037a | 1.000±0.000a | 0.393±0.066a |
| 2 | 0.225±0.058b | 0.047±0.022ab | 0.363±0.073b | 0.797±0.220ab | 0.512±0.119a | |
| 3 | 0.317±0.077c | 0.071±0.019b | 0.473±0.066c | 0.719±0.194b | 0.655±0.088b | |
| 2 | 1 | 0.111±0.033a | 0.038±0.011a | 0.251±0.053a | 0.954±0.095a | 0.470±0.094a |
| 2 | 0.152±0.025a | 0.040±0.007a | 0.304±0.037a | 0.930±0.088a | 0.490±0.078a | |
| 3 | 0.223±0.046b | 0.058±0.012b | 0.389±0.054b | 0.892±0.190a | 0.609±0.070b | |
| 3 | 1 | 0.103±0.039a | 0.031±0.010a | 0.243±0.093a | 0.933±0.190a | 0.434±0.063a |
| 2 | 0.156±0.074ab | 0.039±0.010a | 0.315±0.127ab | 0.939±0.072a | 0.466±0.166a | |
| 3 | 0.199±0.044b | 0.062±0.016b | 0.431±0.071b | 0.875±0.231a | 0.562±0.109a |
Table 3
Silhouette values for different numbers of groups
| Number of groups | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| Silhouette value | 0.653 | 0.623 | 0.628 | 0.514 | 0.474 | 0.399 | 0.453 | 0.361 | 0.360 |
Table 4
k-means clustering (k=2) on sets of the variables vectors (v, φ, γ, ε, and α) characterizing the escape behavior for (Si, θj) where i, j=1, 2, or 3
| (S, θ) | Percentage belonging to each group (%) | |
|---|---|---|
|
|
||
| Group 1 | Group 2 | |
| (1, 1) | 0 (0.0) | 9 (100) |
| (1, 2) | 1 (10.0) | 9 (90.0) |
| (1, 3) | 1 (10.0) | 9 (90.0) |
| (2, 1) | 3 (42.9) | 4 (57.1) |
| (2, 2) | 0 (0.0) | 5 (100) |
| (2, 3) | 2 (20.0) | 8 (80.0) |
| (3, 1) | 8 (88.9) | 1 (11.1) |
| (3, 2) | 5 (71.4) | 2 (28.6) |
| (3, 3) | 7 (70.0) | 3 (30.0) |